Метод решения тепловой задачи для моделирования процесса проплавления при комбинированном лазерном воздействии
Научная библиотека 22.11.2017 Комментариев к записи Метод решения тепловой задачи для моделирования процесса проплавления при комбинированном лазерном воздействии нетАрутюнов Ю.А., Дробязко А.А., Чащин Е.А., Шилов И.В., Шашок П.А. // Фундаментальные исследования. – 2017. – № 8-1. – С. 14-20; УДК 621.789
Работа направлена на решение задачи совершенствования существующих методов решения тепловой задачи для моделирования процесса проплавления при комбинированном лазерном воздействии парциальными источниками модулированного излучения нс-длительности и плавящего излучения импульсом мс-длительности. В работе приведены результаты исследований применительно к воздействию комбинированного лазерного излучения, включающего цуг нс-импульсов с интенсивностью воздействия порядка 1 ГВт/см2, разработан способ формирования многомерной локально измельчающейся сетки для искривленной расчетной области и экономичный алгоритм решения на этой сетке нестационарной тепловой задачи. Показано, что предложенная адаптивная локально изменяющаяся расчетная сетка позволит в области термического воздействия, динамически искривляемой растущим парогазовым каналом, моделировать сугубо нестационарные тепловые процессы, обусловленные многократным скоростным изменением пространственных и временных параметров лазерного излучения, что особенно характерно для сварки металлов комбинированным лазерным излучением.
Стыковая сварка алюминиевых сплавов остается одной из актуальных технологических задач, что вызвано сложностью получения качественных сварных соединений из-за наличия на поверхности тугоплавкой окисной пленки [1]. Одним из способов сварки алюминиевых сплавов является сварка парциальным действием модулированного излучения, удаляющего пленку окислов и одновременно формирующего первоначальный парогазовый канал проплавления (ПГК), и плавящего импульса, воздействие которым производится непосредственно до появления повторно слоя окислов, т.е. до остывания поверхности материала ниже температуры плавления [2]. Применение комбинированного лазерного воздействия для сварки деталей из сплава Амг6 (Al-Mg), по сравнению со сваркой только излучением в режиме свободной генерации, позволяет увеличить глубину проплавления в 2–3 раза при одновременном снижении пористости сварного соединения в 1,5–5 раза с 0,7–0,9 % до 0,4–0,5 % [3]. Приведенные результаты были получены при использовании лазерной установки типа «Квант-15», режим свободной генерации которой имеет многомодовый характер и, как следствие, вариативность распределения интенсивности в зоне лазерного воздействия. Поэтому для анализа режимов обработки в большинстве случаев достаточным являлось использование известных аналитических зависимостей, составленных для стационарных режимов лазерной обработки [3]. При этом размеры и форма ПГК задавалась изначально в условиях задачи: либо правильной фигурой вращения [4], либо по результатам экспериментальных наблюдений [5], и лишь отчасти параметры ПГК итерационно уточнялись в процессе моделирования [5, 6]. Это позволяло выполнять решение задачи оптимизации режимов лазерной обработки только по критерию постоянства температуры поверхности в течение действия импульса. Современные лазерные установки имеют одномодовый характер [7], что позволяет при сохранении энергетических параметров лазерного воздействия обеспечить высокую повторяемость лазерного термического воздействия в зоне обработки. Это делает актуальным выполнение математического анализа c учетом динамического изменения, под действием модулированного лазерного излучения, ПГК для решения задачи оптимизации энергетических затрат лазерного излучения.
Научная новизна
При сварке комбинированным излучением использование известных итерационных моделей [5, 6, 8] затруднено, т.к. учет границ изменения ПГК во время воздействия высокоинтенсивного излучения цуга нс-импульсов 108–109 Вт/см2 приводит к необходимости построения расчетной сетки вблизи облучаемой поверхности с малым итерационным шагом, и сохранение этого шага для описания воздействия излучением мс-импульса с энергией до 15 Дж [3] сопровождается значительными затратами машинного времени. А построение расчетной сетки по критерию постоянства температуры поверхности в течение действия плавящего импульса миллисекундной длительности затрудняет учет сверхградиента поверхностной температуры и развитие ПГК, возникающего в локальной зоне под действием модулированного излучения наносекундной длительности. Таким образом учет нестационарных фаз возникновения и развития ПГК традиционными математическими моделями затруднен сочетанием, во-первых, сложности решения тепловых задач на расчетной области с неправильной формой и быстроизменяющимися внешними границами и, во-вторых, высокоскоростным изменением граничных условий на этих движущихся границах и, прежде всего, масштабным изменением энергетического баланса.
При моделировании процессов проплавления материалов комбинированным лазерным лучом, объединяющим в себе высокоинтенсивное излучение цуга нс-импульсов и мощное излучение мс-импульса [3], добавляется сочетание сверхградиента поверхностной температуры (при воздействии нс-импульсов с интенсивностью 108–109 Вт/см2) и значительной глубины прогрева (при миллисекундном лазерном воздействии). Первый фактор требует чрезвычайного уплотнения расчетной сетки вблизи обучаемой поверхности, а второй фактор – больших размеров непосредственно расчетной области. Получается сугубо нерегулярная и постоянно деформируемая расчетная сетка, для которой нет экономичных методов решения тепловых задач [9].
В работе предложен способ формирования 2-мерной локально-измельченной сетки, позволяющей непрерывно во времени решать тепловую задачу сварки алюминиевых сплавов комбинированным лазерным излучением.
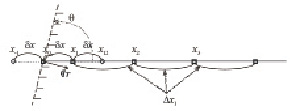
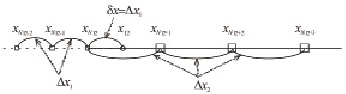
Рассмотрим способ формирования многомерной локально измельченной сетки (ЛИС). Для определения возможности сокращения затрат машинного времени и одновременно достижения 2-го порядка точности расчетной схемы рассмотрим решение одномерной тепловой задачи в приближении расчета на изолированном одномерном тепловом стержне. На рис. 1, а представлен фрагмент поверхности канала, наклоненной относительно оси х на угол θ.
Нулевой узел находится на расстоянии δх от 1-го узла, которое может быть существенно меньше, чем Δx1 – размер следующих за 1-м узлом регулярных шагов сетки. Условие δх ≤ Δx1 возникает из-за движения 0-го узла, вызванного смещением фронта испарения или движением поверхности расплава при его вытекании из ПГК. Запишем в общем виде одномерное дифференциальное уравнение (ДУ) теплопроводности:
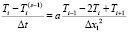 , (1)
, (1)
где Ti – временные производные температуры.
В выражении (1) вторая производная по координате х выражена через узловые значения Ti-1, Ti и Ti+1 на регулярной сетке (см. рис. 1) с постоянным шагом Δx1, а 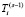 – температура в i-м узле в предыдущий расчетный момент времени s – 1.
– температура в i-м узле в предыдущий расчетный момент времени s – 1.
Для 0-го узла вторую производную удобно записать через центральную конечную разность с шагом δх:
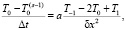 (2)
(2)
где T-1 – мнимый узел одномерной сетки.
Введем граничные условия (ГУ):
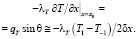 (3)
(3)
При выполнении условий (3) мнимый узел одномерной сетки может быть выражен
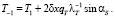 (4)
(4)
С учетом подстановки (4) выражение (2) удобно записать как
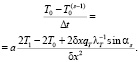 (5)
(5)
Тогда решение уравнения (5) имеет вид
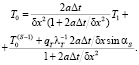 (6)
(6)
При i = 0 уравнение теплопроводности (1) с учетом ГУ (2–6) принимает известный вид [10], что подтверждает допустимость сделанных упрощений:
![]() (7)
(7)
где χ0 и η0 – нулевые прогоночные коэффициенты.
а
б
Рис. 1. Неоднородность ЛИС: а – у границы ПГК (фронта испарения); б – в точке сопряжения измельченной (шаг Δx1) и укрупненной сетки (шаг Δx2). θ – угол наклона поверхности канала, относительно оси х; qT – нормальный к поверхности тепловой поток; x0, x1, x2 и x3 – координаты узлов нерегулярной одномерной сетки с неоднородностью у 1-го узла; x12 – вспомогательный узел; 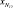 – узел стыковки сеток (2-й узел неоднородности ЛИС); x12 – вспомогательный узел
– узел стыковки сеток (2-й узел неоднородности ЛИС); x12 – вспомогательный узел
Рассмотрим уравнение теплопроводности для 1-го узла сетки (см. рис. 1), который является точкой неоднородности. Введем промежуточный узел х12, в котором узловое значение температуры зададим путем ее интерполяции по 3-м узловым значениям T0, T1 и T2. Для этого используем интерполяционный многочлен Лагранжа 2-го порядка точности L2(x) относительно трех узловых значений аппроксимируемой функции
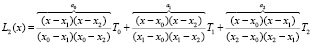 , (8)
, (8)
где
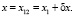 (9)
(9)
Несложно видеть, что выражение (8) является линейной комбинацией трех узловых значений T0, T1 и T2, т.е.
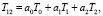 (10)
(10)
где значения a0, a1 и a2 находятся по (8) и (9).
Тогда для узла 1-го узла сетки i = 1 (точки неоднородности сетки) уравнение (1) можно привести к линейному виду:
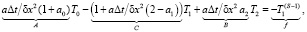 (11)
(11)
совпадающему с каноническим [10] для метода прогонки представлением одномерного уравнения теплопроводности
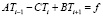 .
.
При i ≥ 2 расчет ведется на регулярной ЛИС с шагом Δx1, в этом случае
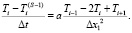 (12)
(12)
Уравнение (12) удобно привести к каноническому, линейному относительно 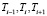 , виду
, виду
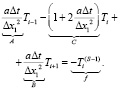 (13)
(13)
При i = N12 возникает еще одна точка неоднородности ЛИС, где регулярная локально измельченная сетка с постоянным мелким шагом Δx1 сопрягается также с регулярной сеткой с постоянным крупным шагом Δx2. На рис. 1, б представлен фрагмент расчетного теплового стержня (параллельного оси х) вместе с точкой неоднородности i = N12. В рассмотренном приближении ( см. рис. 1, б) температура во 2-м вспомогательном узле x12 может быть определена с помощью интерполяции Лагранжа L2(x) по (8) и (10), с учетом
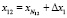 . (14)
. (14)
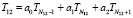 , (15)
, (15)
где при вычислении а0, а1 и а2 вместо координат узлов с индексами 0, 1 и 2 следует использовать координаты узлов с индексами N12-1, N12 и N12+1, а при вычислении линейных коэффициентов A, B, C и f вместо δх использовать Δx1.
Аналогично вышеизложенному, в 1-м узле неоднородности ЛИС, использование интерполяции Лагранжа обеспечивает в узле с индексом N12 сохранение 2-го порядка точности. При i > N12 расчет выполняется на регулярной сетке с шагом Δx2. Таким образом, для одномерного расчетного теплового стержня, содержащего несколько точек неоднородности сетки, показана возможность сквозного применения экономичного метода прогонки при решении тепловой задачи со 2-м порядком точности. Для подтверждения данного вывода была проведена проверка точности решения тепловой задачи при постоянном тепловом воздействии с интенсивностью 0,1 ГВт/см2 путем сравнения с известным аналитическим решением [11]
 . (16)
. (16)
Результаты расчета приведены на рис. 2.
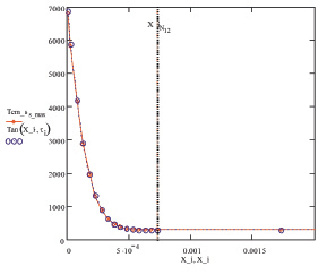
Рис. 2. Температуры в узлах расчетного теплового стержня по координате x, определенные численно (Tem_s, К) и аналитически (Tan, К) для импульса с тепловой интенсивностью qt = 0,1 ГВт/см2 и длительностью τi = 20 нc. X_i – вектор координат узлов ЛИС, см; X_iN12 – координата стыковки мелкой и укрупненной сетки
Видно, что имеет место качественное и количественное совпадение результатов в узлах расчетного теплового стержня Ti для конца 20 нc импульса с тепловой интенсивностью qt = 0,1 ГВт/см2. Размеры пространственных шагов ЛИС составляли: δх = 0,25 мкм, Δx1 = 0,5 мкм и Δx2 = 10 мкм. ЛИС с координатами узлов в векторе X_i – содержала 15 измельченных (N12 = 15) и 35 укрупненных шагов. Относительная погрешность численного решения в сравнении с аналитическим решением уравнения теплопроводности была определена как
 . (17)
. (17)
На рис. 3. показано сравнение погрешностей численного решения на исходной и уплотненной в 2 раза сетке.
Видно (см. рис. 3) что при уплотнении нерегулярной ЛИС в 2 раза, получено снижение погрешности результатов моделирования до 4 раз. То есть реализованная для одномерного случая схема решения тепловой задачи конечно-разностным методом имеет 2-й порядок точности относительно размера пространственного шага. Таким образом, приведенный способ решения одномерной тепловой задачи на нерегулярной адаптивной сетке с использованием трех точечной интерполяции по Лагранжу обеспечивает сочетание 2-го порядка точности и сокращение затрат машинного времени, присущего методу прогонки.
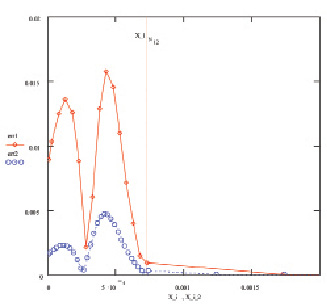
Рис. 3. Погрешности численного решения на исходной (err1) и уплотненной сетке (err1). X_i, X_i_2 – вектор координат узлов исходной и уплотненной в 2 раза ЛИС, см; X_iN12 – координата стыковки мелкой и укрупненной сетки
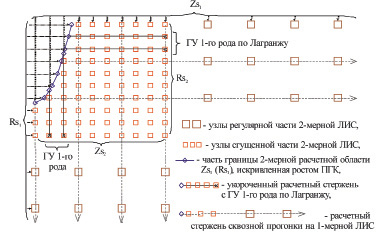
Рис. 4. Фрагмент неоднородной ЛИС у границы ПГК (фронта испарения). Zs1 и Rs1 – внешняя граница ЛИС; Zs2 и Rs2 – граница сопряжения сгущенной сетки и регулярной части ЛИС
Рассмотрим способ формирования 2-мерной ЛИС, позволяющей решать тепловую задачу при существенно неоднородных параметрах лазерного воздействия, имеющих место при комбинированном лазерном воздействии. На рис. 4 приведен фрагмент неоднородной ЛИС у границы ПГК, возникающего при движении фронта испарения за один нс-импульс. Видно, что строки или столбцы узлов измельченной сетки, примыкающие к строкам/столбцам регулярной сетки, образуют сквозные расчетные стержни, на которых вышерассмотренным методом решается одномерная тепловая задача. Выбрав одно из направлений (по z или по r) и выполнив прогонки во всех «сквозных» расчетных стержнях, мы получим в этих стержнях обновленные узловые температуры, включая значения в узлах неоднородности ЛИС по границе Zs2 или Rs2. На 2-мерных границах Zs1 и Rs1 для сквозных и укороченных расчетных тепловых стержней наиболее естественным граничным условием будет ГУ 2-го рода с заданием параметров поглощения ЛИ и испарения материала:
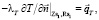 (18)
(18)
где
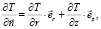
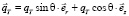 .
.
Тогда для прогонок по направлению r ГУ 2-го рода принимают вид
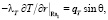 (19)
(19)
а для прогонок по направлению z
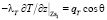 . (20)
. (20)
Известно [10], что при использовании метода переменных направлений вычисления поперечной производной 2-го порядка не требуется, а значит, для каждого конкретного расчетного стержня (см. рис. 4) из распределения температур, полученных при предыдущей ортогональной прогонке, необходимо определить одно узловое значение температуры на поверхности, т.е. внешнем крае расчетного стержня, которое удобно получить интерполяцией вдоль границ Zs1 или Rs1 по достаточно большому количеству узлов. В работе полагали, что границы Zs2 и Rs2 отдалены от зон максимальных градиентов температур и интенсивного перераспределения тепловых потоков. Это приближение позволяет считать, что аппроксимация температурного распределения вдоль этих границ хорошо выполняется по узловым значениям ЛИС с крупным шагом, т.е. по значениям температур на сквозных расчетных стержнях по границам Zs2 и Rs2. Таким образом на крайних узлах укороченных расчетных тепловых стержней сгущенной части ЛИС, которые обрываются на границах Zs2 и Rs2, с помощью интерполяции Лагранжа можно задать фиксированные на данный момент времени температуры, т.е. определить для укороченных расчетных тепловых стержней по границам Zs2 и Rs2 ГУ 1-го рода.
Следует отметить, что если соответствующая подмодель не обеспечивает вычисления баланса поглощения и испарения с мелким шагом ЛИС, то в этом случае допустимо интерполировать температуру на границах Zs1 и Rs1, т.е. так же, как и для узлов на границе Zs2 и Rs2 можно задать ГУ 1-го рода. В этом случае узлы сгущенной сетки, которые продолжаются на линиях регулярной сетки за границами Zs2 и Rs2, участвуют в тепловом расчете, образуя вместе с разреженными узлами регулярной сетки глобальные тепловые стержни с протяженностью от облучаемой поверхности и до удаленной границы расчетной области. При этом расчетные тепловые стержни сгущенной тепловой сетки, обрывающиеся на границах Zs2 и Rs2, должны заканчиваться узлами, где ГУ следует задавать принудительно, например с помощью аппроксимации по Лежандру L2 на базе тех узлов сгущенной сетки на границах Zs2 и Rs2, которые участвуют в глобальных тепловых стержнях. Отметим, что при этом все внутренние узлы становятся взаимосвязанными. Таким образом проводя расчет одной из координат, сначала «прогоняются» сквозные тепловые стержни. Затем по полученным узловым значениям температуры Т на границах Zs2 или Rs2 путем интерполяции задаем граничные узловые значения в качестве ГУ первого рода на коротких тепловых стержнях сгущенной тепловой сетки.
Заключение
В работе применительно к воздействию комбинированного лазерного излучения, включающего цуг нс-импульсов с интенсивностью воздействия порядка 1 ГВт/см2, разработан способ формирования многомерной локально измельчающейся сетки для искривленной расчетной области и экономичный алгоритм решения на этой сетке нестационарной тепловой задачи. Показано, что адаптивная ЛИС позволит в расчетной области, динамически искривляемой растущим ПГК, моделировать сугубо нестационарные тепловые процессы, обусловленные многократным скоростным изменением пространственных и временных параметров лазерного излучения, что особенно характерно для сварки металлов комбинированным лазерным излучением.


Leave a comment
You must be logged in to post a comment.